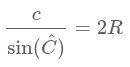Em meu cotidiano, uso a Lei dos Senos?
Neste artigo mostramos um exemplo de matemática que é útil, mas será que esta matemática é uma matemática de nosso cotidiano, de nosso dia-a-dia? É sobre isso que falaremos nesta postagem.
Observe a situação mostrada abaixo. Como
poderíamos calcular a distância entre as margens? Vamos ver o tipo de ferramenta que necessitaríamos para executar esta tarefa? | ||
| ||
As ferramentas necessárias serão: uma trena, um teodolito (pode ser um feito em casa mesmo) e um pouco de trigonometria. ;-) A imagem anterior fica no Lago Paranoá em Brasília e você pode ver o local e fazer medidas usando o Google Earth. Assim como mostra o desenho, vamos supor que estejamos ao lado da piscina (canto esquerdo da imagem) em um ponto que chamaremos ele de ponto A. Escolhamos um ponto de referência do outro lado da margem que pode ser uma das três árvores. Vamos dizer que esta margem fica em um ponto B. Feito isso, vamos andar ali perto da piscina até lado de cima e ali será o nosso ponto C. Teremos algo como mostra a figura seguinte | ||
| ||
Se você está na margem esquerda (onde estão os pontos A e C), com a trena você pode medir essa distância, certo? Ao fazer essa medida, você encontrará cerca de 33 metros. Estando em A, aponte o Teodolito para C e depois gire-o até que ele esteja apontando para B (do outro lado da margem). Quanto mais preciso for essa medida, mais preciso será a distância AB, que procura. O ângulo que encontrará em Ĉ será de aproximadamente 80º. Dirija-se ao ponto C e aponte o Teodolito para o ponto A e gire-o até que ele esteja apontando para o ponto B. Faça essa medida com muito cuidado. Deverá encontrar um ângulo próximo de 96,5º. Com isso tem agora o ângulo Â. Para encontrar o ângulo B, basta notar que a soma dos ângulos internos de um triângulo plano é de 180º. Não é difícil perceber que como | ||
80+96,5+B=180 | ||
então B=3,5º. Carregando a imagem acima no GeoGebra encontramos ângulos mais precisos (ver imagem a seguir), mas com um teodolito caseiro, não conseguirá essa precisão. Vamos ficar com os números apontados, que são aproximações mencionadas anteriormente. | ||
| ||
Então, a pergunta é: com esses dados, conseguimos saber a distância entre os pontos A e B? Essa distância nos informará a distância entre as margens que procuramos | ||
Apenas uma pequena observação | ||
Depois que desenvolvermos a ferramenta matemática para fazer esse cálculo, verá que a precisão do resultado dependerá da precisão dos instrumentos que não dão as informações de distância (entre os pontos A e C - isso não é problema) e os ângulos e nosso resultado será cada vez mais preciso na medida em que tivermos a precisão dessas medidas. A ferramenta matemática que usarmos chama-se Lei dos Senos e vamos entender e deduzir essa lei a seguir. No final da postagem, iremos resolver o problema de calcular a distância apresentado no início desta postagem. | ||
A lei dos Senos | ||
Nestas breves notas eu me proponho a falar sobre o uso do software GeoGebra para estudar a Lei dos Senos e os cuidados que devemos ter a respeito de demonstrações. O software ilustra muito bem, mas ele prova alguma coisa? Veja com o software pode ajudar o aluno a perceber o que diz a lei dos senos. Diz esta lei que para qualquer triângulo ABC a medida de um lado dividido pelo sendo do ângulo que é oposto a este é igual não importa qual lado você toma e o resultado da divisão é sempre igual ao dobro do raio "R" da circunferência que circunscreve o triângulo. Em outras palavras o que este resultado diz é que: | ||
| ||
Note que com palavras isto não diz muito a alguém que está vendo pela primeira vez isto. Entretanto, se este aluno puder ver uma ilustração mostrando isto gravará mais facilmente o resultado (penso eu). Veja um exemplo (clique na imagem para vê-la ampliada). Agora imagine se ele (ou você) pudesse agarrar um dos vértices e arrastar e automaticamente esta ilustração puder ir sendo atualizada... Isto é o que o GeoGebra permite que se faça... Visualizar centenas de ilustrações em alguns segundos e observar o sentido do que está estudando... A imagem que vê abaixo é uma imagem dinâmica gerada pelo software GeoGebra. Clique sobre um dos vértices e arraste-o. O que pode ver com o texto dinâmico? Imagine seu aluno vendo isto. O que você acha quanto à compreensão do que diz a Lei dos Senos. O texto acima diz o mesmo que a imagem abaixo. Sem dúvidas ele irá lembrar da imagem, concorda. | ||
| ||
Arraste os pontos A, B ou C e veja o que acontece com a relação | ||
| ||
Entretanto, não devemos esquecer que imagem não prova nada. Ela apenas ilustra (mesmo esta dinâmica). Softwares como o GeoGebra devem ser usados em sala de aula, mas não como mecanismo de demonstração pois ele não demonstra nada. Entretanto, é fato que ele permite entender melhor as relações que temos. Este mesmo software pode ser usado para conduzir o estudante para a demonstração deste resultado. Abaixo há uma pequena modificação no arquivo acima e foi preparado para que o aluno percebe o caminho da demonstração. Obs.: na figura seguinte, clique e arraste um dos vértices do triângulo e observe as relações entre os objetos. | ||
| ||
Veja como pode ser a condução: "O" é o centro da circunferência e CD é diâmetro. Isto implica que CDB é retângulo em C. O ângulo em "A" e em "D" têm a mesma medida por estarem em uma circunferência e determinarem o mesmo arco BC Calculando o seno do ângulo em D encontraremos | ||
| ||
e já que o ângulo em D tem a mesma medida que o ângulo em A | ||
| ||
de onde vem que | ||
| ||
Refazendo este raciocínio mas considerando os outros pontos B e C encontraremos que | ||
| ||
e | ||
| ||
de onde vem a fórmula conhecida: | ||
| ||
Solução do problema proposto | ||
Agora que já temos a ferramenta matemática, podemos tentar resolver o problema. Eis os dados: | ||
| ||
Com isso, podemos mostrar a situação assim: | ||
| ||
Só necessitamos dos ângulos opostos às medidas que conhecemos ou queremos descobrir, isto é, precismos dos ângulos Ĉ (oposto à medida que queremos descobrir) e B, oposto à medida que temos (33 m). Pela lei dos senos, | ||
| ||
de onde obtemos, multiplicando ambos os membros por sin(80º) que | ||
| ||
Esta última parte pode ser feita facilmente com a ajuda de uma calculadora científica ou usando uma tabela de senos e cossenos. | ||
Então, esses cálculos nos dizem que a distância de uma margem até outra é de cerca de 532,31 metros. Compare agora com o resultado que a ferramenta Google Earth retorna | ||
| ||
Um erro próximo de 12 metros (para mais). Com uma ferramenta que retornasse valores mais preciso dos ângulos (principalmente) teríamos um valor mais próximo do real. | ||
Usamos Lei dos Senos em nosso dia a dia? | ||
NÃO. NÃO USAMOS. Ao menos não é comum o uso. Entretanto, a Lei dos Senos é útil para cálculo de distâncias que podem ser inacessíveis. Lei dos Senos tem aplicação, mas... Não se trata de algo que usará em seu cotidiano. Entenda que o fato de não usar em seu cotidiano não faz desse conhecimento inútil. Falando nisso, escrevemos três postagem aqui falando sobre isso. Não quer dar uma olhadela? | ||
| ||
Grande abraço | ||
| ||