Folha A4 e Raiz quadrada de 2: qual a relação?

Às vezes eu digo que matemática é como a massa que fica entre os tijolos ou o ferro e concreto que estão ali em uma construção e que é importante para esta construção, mas que ninguém vê. O fato de você não vê uma aplicação imediata não quer dizer que ela não exista e hoje eu quero mostrar a vocês como a √2 está presente em sua vida e você, talvez, não saiba... ;-)

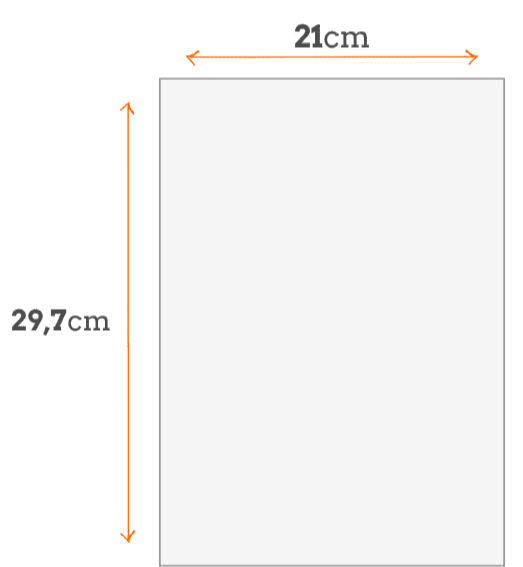
Alguma vez você já parou para reparar nas dimensões da folha A4? Na verdade o que vamos falar aqui não funciona apenas para folhas A4. Também valem para A5, A3, A2, etc. Estas dimensões têm algo em comum. Se você dividir o lado maior pelo lado menor vai encontrar √2. Veja um exemplo de tamanho de folhas A4 como mostra na figura seguinte.

Se dividir 29,7 por 21 encontrará 1,414285714, que é um valor aproximado para √2. Se usar uma calculadora verá que 1,414213562 é o número obtido quando pede para calcular a √2 (que é uma aproximação para este número, pois, como é irracional, não pode ser escrito como um número decimal finito, mas podemos deixar esta discussão mais técnica para outro momento ;-)).

Dobre uma folha A4 ao meio e...

O que acontece quando você dobra uma folha A4 no meio? Deverá ter algo como o mostrado na figura abaixo

Talvez tenha lhe passado despercebido, mas se você olhar para uma folha A4 dobrada ao meio (a metade dela, portanto) é uma miniatura da folha A4 original, ou seja, ela mantém a proporção entre os lados. Em outras palavras, se dividir o lado maior pelo lado menor ainda continuará a encontrar 1,414285714. Se dividir novamente essa folha menor, que já é miniatura da folha A4, encontrará uma folha menor ainda que também será miniatura da maior.

Se pegar o lado maior do quarto da folha A4 e dividir pelo lado menor deste quarto obterá...... Isso mesmo 1,414285714 que é um valor aproximado para √2.

A matemática por trás do que queremos

A matemática por trás dessa mágica de dividir ao meio e obter miniaturas da folha original é simples. Essas dimensões foram pensadas para ser assim. Qual deve ter sido a pergunta original quando se pensou em definir a proporção entre lado maior e lado menor? Penso que deve ter sido algo como

Queremos uma proporção entre lado maior e lado menor de tal modo que estas proporções se mantenham quando a folha for dobrada ao meio.

Bom, uma pessoa com um conhecimento mínimo de matemática deve ter feito um cálculo rápido mais ou menos como segue

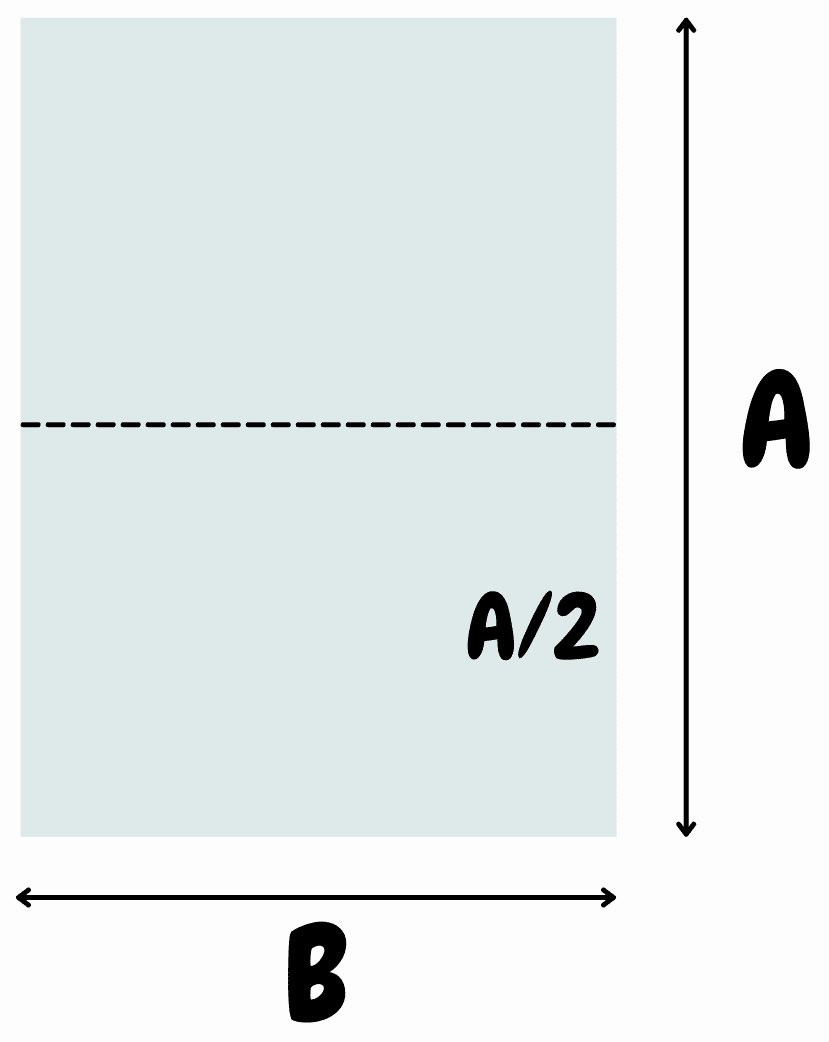
Lembre-se que a característica que se quer é que a razão entre Lado Maior e Lado Menor seja o mesmo, tanto para a folha inteira quando para a sua metade. Podemos escrever assim

Lado Maior da folha maior [A] / Lado Menor da folha maior [B] deve ser igual ao Lado Maior da folha menor [B] / Lado Menor da folha menor [A/2] 

Se isso acontecer teremos a proporção mantida e isso é o que chamamos no início deste texto como uma "miniatura". Se usarmos A para representar a Altura, B para representar a Base podemos "traduzir" para símbolos matemáticos da seguinte forma

A/B=B/(A/2)

Como estamos diante de uma proporção, então o produto cruzado deve dar o mesmo resultado, certo? [A fala correta seria: o produto dos meios deve ser igual ao produto dos extremos] e assim teremos

A²/2=B²

Uma manipulação algébrica simples nos levará para

A²/B²=2

de onde vem que

(A/B)²=2

Agora, extraindo a raiz quadrada em ambos os membros obtemos

A/B=√2

Ou seja, a razão entre a Altura e a Base deve ser... √2... Isso mesmo.  ;-) Então, veja só... Você tem um número irracional presente quase todos os dias em sua vida e talvez não soubesse ainda...

Outros tamanhos de folha

Quando você dobra uma folha A4, você encontra duas folhas menores, certo? Cada uma destas folhas é uma folha A5. Veja na ilustração abaixo

E se você dobrar uma folha A5 ao meio, você encontra uma folha A6 e assim por diante... Veja na imagem seguinte uma ilustração.

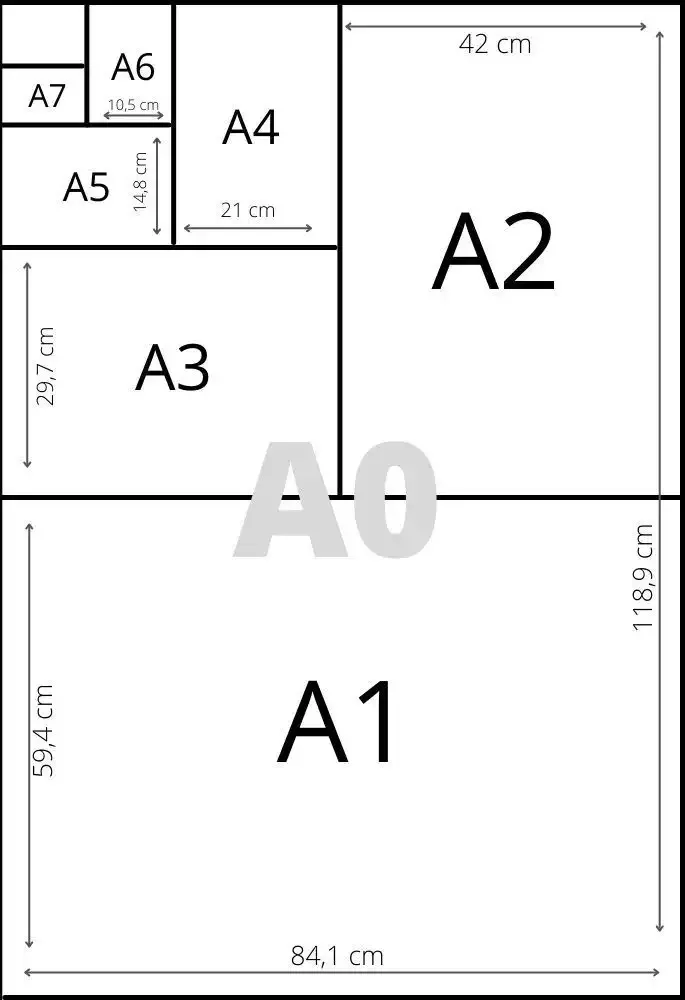
Seguindo esta lógica, como você encontra uma folha A3? Isso mesmo, colocando duas folhas A4 juntas e encontrará uma folha A2 colocando duas folhas A3 juntas e assim por diante... A imagem seguinte ilustra essas relações a partir do tamanho A0.

Interessante, não? Se o tamanho fosse escolhido de uma forma aleatória, não haveria essas versões em miniatura das folhas maiores. Para que isso aconteça, a razão (divisão) entre as medidas do lado maior e do lado menor deve ser igual a √2. ;-)

Abração pro 6

Luís Cláudio LA