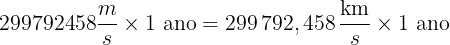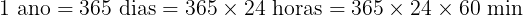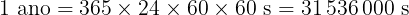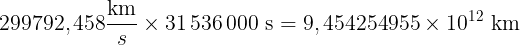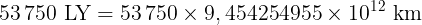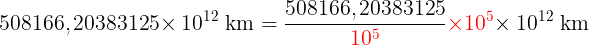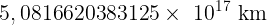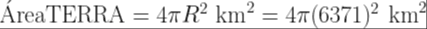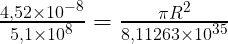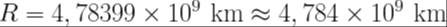CD, Terra e Disco Planetário: qual é a relação?

Eu ouvi durante o episódio Milky Way da série Universo (Netflix) a pesquisadora entrevistada disse que "se o sistema solar tivesse o tamanho de um CD, então a Via Láctea teria o tamanho da Terra". É sobre isso que quero falar neste texto. Vamos checar se vale a proporção que ela sugeriu. ;-)

Ano-Luz em Quilômetros

Um ano-luz é a distância percorrida pela luz em 1 ano. Como sabemos que a velocidade é a razão entre a distância percorrida e o tempo gasto, podemos escrever: velocidade = distância/tempo de onde podemos concluir que

distância=velocidade x tempo

No caso da velocidade da luz temos 299 792 458 m / s em um tempo de 1 ano. Então, substituindo na relação acima teremos

distância=velocidade x tempo=299 792 458 m / s . 1 ano

Hmmm.... Está meio feio esse número, não? Vamos tentar colocar a distância em quilômetros. Para isso, vamos precisar transformar o que está em metro em quilômetro e o que está em ano em segundos. Vamos lá... Sabemos que 1000 m = 1 km, certo? Então

Para dividir por 1000 basta andar com a vírgula três casas para a esquerda e como 1000 m = 1 km ficaremos com

Assim, a distância que a luz percorre em um ano é, até o momento

Agora, precisamos transformar 1 ano em segundos. Vamos considerar que 1 ano = 365 dias. Acompanhe o raciocínio

o que finalmente nos dá

Deste modo, a distância percorrida pela luz em um ano será, em quilômetros,

Assim, se usarmos 'LY' (Light-Year) como símbolo para Ano-Luz podemos dizer que

Área da Via-Láctea

Para fonte de informações para os nossos cálculos, usaremos as informações disponível nesta página (para Via Láctea) e nesta (para Sistema Solar). A nossa galáxia, a Via Láctea,tem a forma espiralada que pode ser distribuída em um disco de cerca de 105.700 anos luz de diâmetro e aproximadamente 3000 anos luz de espessura. Aqui vamos nos concentrar no diâmetro e em particular no raio, pois vamos pensar nela como um disco de raio R=105.700/2=53750 anos luz. 

Precisamos do raio da Via-Láctea em Quilômetros, mas a partir do que vimos na seção anterior, não é difícil fazer esta conversão. Para tal, observe que

de onde vem que

ou seja, o raio da Via-Láctea é de 

Isso é tão grande que não dá para imaginar uma distância desta.... Assim, a Via Láctea tem uma área de aproximadamente

isto é, em notação científica temos

Agora, vamos ao cálculo da área da Terra.

Área da Terra

A Terra é praticamente uma esfera. A rigor é um elipsoide em que a maior distância do centro até a superfície difere em pouco mais de 20 km que em relação ao raio da terra que é de aproximadamente 6.371 km que dá uma diferença de cerca de 0,313%. Há um texto que eu escrevi em que tento mostrar que a Terra é mais lista do que uma bola de bilhar e você pode ler esse texto AQUI, se você quiser. Então, vamos considerar a Terra como uma esfera de raio R=6371 km. Como a área de uma esfera é 4π.R² então teremos

Fazendo os cálculos e colocando em notação científica concluiremos que

Note que aqui usamos o fato de que o volume da esfera de raio R é 4π.R². Você achou que isso seria inútil e não serviria para nada, certo? Pois é, serve para calcular a área da superfície terrestre. E quanto ao Sistema Solar?

Área do Sistema Solar

Aqui vamos ter que fazer algumas considerações, pois o Sistema Solar pois a forma do Sistema Solar não é algo que se saiba exatamente como é. Veja esta reportagem que fala um pouco sobre isso. Segundo a matéria o Sistema Solar teria a forma de um Croissant amassado

Grande parte dessas ideias se baseia em informações enviadas pela sonda Cassini, que estudou Saturno entre 1997 e 2007, e em dados provenientes das sondas Voyager 1 e 2, que foram lançadas em 1977 e são as únicas a já terem chegado ao espaço interestelar. (...) Outro equipamento essencial para o estudo foi a sonda New Horizons, lançada em 2006 com objetivo de investigar Plutão.

Como esta forma do Sistema Solar é um tanto "estranha", vamos fazer o seguinte: olharemos para a área de um CD, para a área da Terra e depois até onde teríamos que ir pensando no sistema solar na forma de um disco com o Sol no centro. Tudo bem, não é, como viu logo acima, mas vamos pensar nesta simplificação.

Área de um CD

Um CD (Compact Disc) tem cerca de 12 cm de diâmetro (veja dimensões exatas na figura seguinte).

Naturalmente, a área deste CD é de π.R² cm²=π.12² cm²=π.144 cm²=452,389342117 cm². Pois bem, agora precisamos da área do CD em km. Isso mesmo...

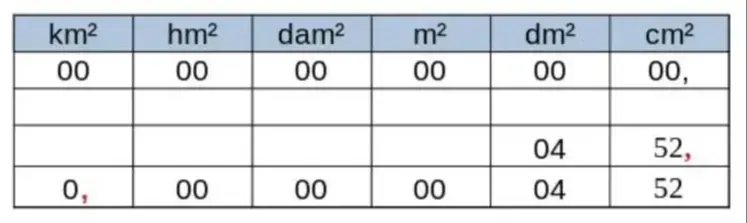
Para transformar cm² em km², basta andar com a vírgula para a esquerda 10 casas decimais, como mostramos na tabela de transformação a seguir

Então vamos lá... A área do CD em km² será 0,0000000452 km² que em notação científica ficará

Vamos encontrar o "Raio" do Sistema Solar de modo que a seguinte proporção seja válida

[Área do CD] está para [Área da Terra] assim como [Área do Sistema Solar] está para [Área da Via Láctea]

que podemos escrever assim

Substituindo os valores que encontramos acima teremos

Note que como as unidades de medidas são as mesmas, não precisaremos escrevê-las e assim ficaremos com

Agora, vamos resolver esta equação em R. Esse R é o raio do disco planetário, vamos assim chamar, medido a partir do Sol, tomado aqui como centro. Vejamos onde esse disco teria suas bordas. Vamos usar um software para nos ajudar com esse cálculo. Veja os comandos a seguir.

Então, encontramos que para que esta proporção funcione, precisamos considerar a nossa fronteira do disco planetário a

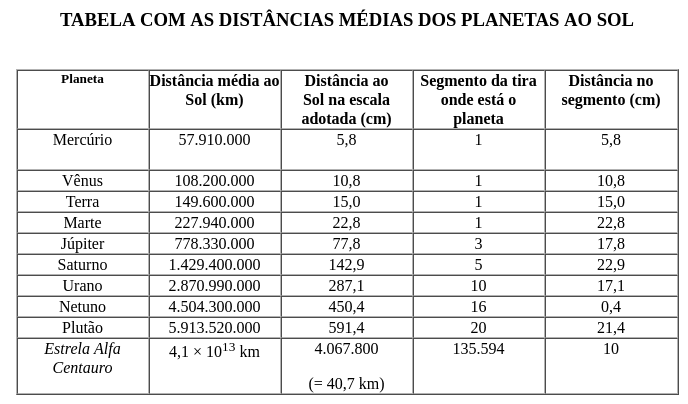
Vamos ver uma tabela com a distância do Sol até os planetas (conhecidos) do Sistema Solar

O valor que encontramos para R coloca o nosso disco depois de Netuno que é aproximadamente 4,5.10^9 e Plutão (que não é mais considerado planeta, mas em nossos corações sempre será um planeta. ;-)) aproximadamente 5,9.10^9. Veja que o nosso R é aproximadamente 4,7.10^9.

Conclusão

Salvo eu ter errado em alguma conta, a pesquisadora fez menção ao Sistema Solar na comparação que ela fez, mas aqui só conseguimos mostrar que a comparação faz sentido olhando para o disco planetário. Entretanto, isso não tira o mérito da comparação que ela fez trazendo para algo que conseguimos ter uma ideia com os sentidos humano algo que sabíamos que era grande, mas essa comparação realmente faz com que percebamos como somos pequenos

Faça um exercício. Pegue um CD em suas mãos. Imagine que neste CD você tem todos os planetas conhecidos do Sistema Solar em suas mãos. A área desse disco planetário está em suas mãos, mas esse disco está em um sistema maior chamado Via Láctea em que a área é próximo à área da Terra. Consegue perceber agora o tamanho da Via Láctea? E ela nem é a maior... Isso não é fantástico?

Isso suscita outra discussão. Se existisse outra pessoa no outro bairro da sua cidade, quais as chances de se comunicarem? E se esta outra pessoa estivesse em outra cidade? Lembre-se de que um CD é onde estão todos os planetas conhecidos do Sistema Solar. Você poderia se comunicar com eles? E se esta outra pessoa estivesse em outro país, em outro continente ou do outro lado da Terra? É por isso que eu digo que pode até existir outras civilizações inteligentes na Via Láctea, mas estamos separados pela distância. Mas isso é assunto para outra postagem.

Exercícios para casa: as sondas Voyager 1 e 2 estão a uma distância da Terra que gira em torno das 75 UA (Unidade Astronômica) em que 1 UA corresponde à distância da Terra ao Sol, cerca de 150 milhões de quilômetro ou seja, 1 UA= 1,5.10^8 km. Quantos cm a sonda se afastou da borda do nosso disco planetário (que é o nosso CD)? Lembre-se que foram cerca de 45 anos para percorrer esta distância.

A propósito... Se quiser ver alguém que escreve muito bem sobre um possível contato nesta vastidão do universo, considere ler o livro a seguir

Último comentário

Aqui você pode notar que usamos algumas coisas que se aprende na escola. Eis os assuntos que você estudou na escola e que estão aqui

1. Notação Científica
2. Razão
3. Proporção
4. Transformação de Unidades de Medida

Talvez você não use toda a matemática que estuda em seu cotidiano, mas isso não faz dela inútil. Aplicações sempre existem. ;-)

Grande abraço

Luís Cláudio LA